|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Я уже давал в "Забавных задачках" ссылку на лекцию Арнольда, но там обсуждение не занялось. Что правильно, так как формат не тот - поэтому решил выделить в отдельную тему.
Я начну с описания задачи, потом постепенно буду какие-то свои мысли выкладывать и чем больше народу присоединится, тем лучше. Только чур по интернету не рыскать - идея в том, чтобы до чего-нибудь (необязательного нового) дойти самим. Задачка никаких специальных знаний не требует, что приятно.
Итак:
Изучаем такой простенький объект - конечное множество и его отображение в себя. Такому объекту можно сопоставить граф: вершины (точки) соответствуют элементам множества, ребра (стрелочки) идут от элемента к тому элементу, в который его переводит отображение. Из каждой вершины выходит ровно одно ребро, так что ребер в графе столько же, сколько вершин. Граф не обязан быть связным - он может развалиться на несколько кусков. Впрочем, в каждом куске по-прежнему столько же ребер, сколько и вершин, а, значит, в нем есть цикл, причем, ровно один. То есть, наш граф выглядит так: несколько непересекающихся циклов, и из каждой вершины цикла может расти куст.
Теперь собственно задача. Нашим конечным множеством будет набор строк из нулей и единиц длины n, отбражением - взятие производной: замена каждого элемента строки на сумму его и его соседа справа по модулю 2 (к последнему элементу добавляем первый). Вопрос - как выглядит соответсвующий граф, сколько в нем циклов, какой длины, какие из них растут кусты? |
|
|
| |
|
|
Попробовал поискать циклы. Оказалось, что циклов длиной 2^n-1 (два в степени n минус один) не существует. Единственное исключение - цикл длиной 1. Ему соответствует число из одних нулей.
Про циклы другой длины пока ничего сказать не могу. |
|
|
| номер сообщения: 49-25-3198 |
|
|
|
|
MikhailK: Попробовал поискать циклы. Оказалось, что циклов длиной 2^n-1 (два в степени n минус один) не существует. Единственное исключение - цикл длиной 1. Ему соответствует число из одних нулей.
Про циклы другой длины пока ничего сказать не могу. |
Циклы длины 2^n - 1 сушествуют - например, среди последовательностей длины 3 есть цикл длины 3. Они, правда, довольно специальные. А вот циклов длины 2^n действительно не существует. |
|
|
| номер сообщения: 49-25-3199 |
|
|
|
|
| iourique:Циклы длины 2^n - 1 сушествуют - например, среди последовательностей длины 3 есть цикл длины 3. Они, правда, довольно специальные. А вот циклов длины 2^n действительно не существует. |
Ой, я на единичку ошибся. Я имел ввиду циклы длиной 2^n. |
|
|
| номер сообщения: 49-25-3200 |
|
|
|
|
Еще из наблюдений:
изучаемое отображение А - линейно и имеет вид А = 1+Т, где Т - матрица циклической перестановки. Отсюда следует, что А^(2^k) = (1+T)^(2^k) = 1 + T^(2^k). В частности, если длина строки n - степень двойки, то А^n = 0. Это доказывает тот факт, что для степеней двойки граф содержит единственный (тривиальный) цикл. |
|
|
| номер сообщения: 49-25-3201 |
|
|
|
|
Простоял давеча в пробке, кое-что придумалось.
Математики, ногами не бейте, если все это тривиально/очевидно.
Всяк играет, как умеет.
Итак, мысли о кустах, корнях и листьях.
Заметим: A x = A NOT(x) (A – это наше отображение, NOT – побитовое инвертирование), т.е. x и его «инверсия» дают один и тот же образ (это следует из того, что операнды XOR-а можно инвертировать без изменения результата).
Отсюда следует, в частности, что точка и ее «инверсия» не могут лежать на одном цикле (образ-один!), а значит, как уже говорилось, циклов длины 2^n быть не может (у каждой точки цикла есть инверсия, лежащая вне его).
Логично предположить, что любая точка имеет или 2 прообраза, или ноль.
Займемся «интегрированием».
Пусть b = {b[0] b[1] ... b[n-1]} – некая точка (b[i] – биты двоичного представления).
Будем искать ее прообраз a: b = A a.
Придется выбрать “константу интегрирования” a[0] = 0 (для определенности). Остальные биты a легко находятся a[i+1] = XOR(a[i], b[i]).
Ну, т.е. a[1] = XOR(a[0], b[0]) = XOR(0, b[0]) = b[0];
a[2] = XOR(a[1], b[1]) = XOR(b[0], b[1]), и т.д.
Так мы доберемся до «лишнего» бита: a[n] = XOR(b[0], b[1], ... b[n-1)).
Теперь возможны два случая:
1) a[n] = 0 = a[0] – все сошлось – мы нашли нужный прообраз a = {a[0] a[1] ... a[n-1]};
кстати, если бы «константой интегрирования» мы выбрали c[0] = 1, то получили бы c = NOT(a) – тоже прообраз. Других прообразов нет.
2) a[n] = 1 не равно a[0], противоречие, прообраза нет.
Осталось заметить, что a[n] = XOR(b[0], b[1], ... b[n-1)) – это остаток от деления на 2 числа единиц в бинарной записи b.
Т.е. если это число четное, то прообраз есть (точнее, есть два прообраза); а если нет – то и прообразов никаких нет.
Получился простой признак «листа» (точки без прообразов): в его бинарном представлении имеется нечетное число «единиц».
Тут, наверное, и дальше можно копать.
Например, у нуля всегда два прообраза: он сам и число из всех единиц: 11...1. Если n – нечетное, то у 11...1 прообразов нет, и дальше отсюда ничего не растет.
Ну вот пока и все. |
|
|
| номер сообщения: 49-25-3202 |
|
|
|
|
Ваши рассуждения можно продолжить и показать, что если длина строки - нечетное число, то ровно половина элементов находится в циклах:
У каждой строки с четным числом единиц, как Вы показали, есть два прообраза - в одном из них четное число единиц, в другом нечетное. Это значит, что у любой строки с четным числом единиц есть прообраз с четным числом единиц, и, следовательно, все такие строки находятся в циклах. Наоборот, строки с нечетным числом единиц в цикле лежать не могут (у них нет прообразов), но они попадают в цикл за один шаг.
p.s. Когда Михаил говорил о невозможности циклов длины 2^k он имел в виду любое k, не обязательно совпадающее с длиной строки. |
|
|
| номер сообщения: 49-25-3203 |
|
|
|
|
Еще немного покопаю в ту же сторону:
Пусть длина строки n - составное число, n = kl. Тогда можно определить проекцию
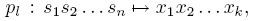
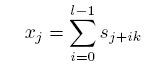
переводящую строки длины n в строки длины k.
Отображение А "коммутирует" с такой проекцией, в том смысле что применяя сначала А, а потом проекцию, или сначала проекцию, а потом А (это другое А, оно живет в другом пространстве) получаешь одно и то же.
Если теперь 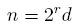 , где d - нечетное число, то проекция , где d - нечетное число, то проекция 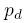 переводит строки длины n в строки длины переводит строки длины n в строки длины 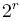 . Как мы уже знаем, отображение А в степени . Как мы уже знаем, отображение А в степени 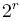 переводит все строки длины переводит все строки длины 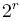 в ноль (строку из одних нулей). Отсюда, отображение А в степени в ноль (строку из одних нулей). Отсюда, отображение А в степени 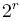 переводит все строки длины n в прообраз нуля при проекции переводит все строки длины n в прообраз нуля при проекции 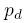 . Это означает, что все строки, принадлежащие циклам, лежат в ядре проекции. Несложно показать, что верно и обратное. . Это означает, что все строки, принадлежащие циклам, лежат в ядре проекции. Несложно показать, что верно и обратное.
p.s. Извините за неровный почерк. |
|
|
| номер сообщения: 49-25-3204 |
|
|
|
|
О циклах длины 2^k - 1. Пусть x принадлежит такому циклу. Тогда
(1+T)x = Ax = A^(2^k)x= (1 + T^(2^k))x, то есть, x = T^(2^k-1)x, а значит х - периодичная строка, с периодом делящим (2^k - 1). Отсюда, например, следует, что цикл длины 3 появляется только в строках, длина которых делится на 3, причем, ровно один раз. Точно так же, циклы длины 7 имеются только в строках, чья длина делится на 7, в количестве 9 штук. |
|
|
| номер сообщения: 49-25-3205 |
|
|
|
|
Продолжу вести дневник наблюдений. Я буду рассматривать строки нечетной длины и ограничусь строками, сумма элементов которых равна нулю. Оператор А на таких строках обратим (они все лежат в циклах). Пусть 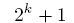 делится на делится на 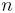 . Тогда . Тогда
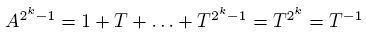 , , и, как следствие,
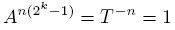 . . Это подтверждает то наблюдение, что длина самого длинного цикла равна длине строки, умноженной на степень двойки минус один. Например, для 11 имеем: 33 делится на 11, значит, А в степени 31*11=341 является тождественным преобразованием. Циклов длины 31 быть не может, так как А в 31 - это сдвиг, циклов длины 11 тоже нет (это чуть хитрее). Значит, все нетривиальные циклы имеют длину 341.
Правда, такая степень двойки, что 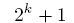 делится на делится на 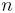 , существует не для всех , существует не для всех 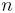 . Примером числа, для которого это не так, является 23. . Примером числа, для которого это не так, является 23. |
|
|
| номер сообщения: 49-25-3208 |
|
|
|
|
Приятель, с которым я поделился задачкой, заметил несложный, но забавный факт:
Выпишем строчку из нулей и единиц длины k. Под ней запишем ее производную, под производной - ее производную, и так далее, пока не зациклимся. Получим матрицу размера k на n из нулей и единиц, отвечающую циклу длины n в строках длины k. Транспонируем эту матрицу и замечаем, что она отвечает циклу длины k в строках длины n. Отсюда получается, например, еще одно доказательство, замеченного Михаилом факта об отсутствии циклов длины степени двойки. Если бы такой цикл был, то был бы и цикл в строках длины степени двойки, а таких циклов нет.
Пример - цикл длины 15 из строк длины 5:
11000
01001
11011
01100
10100
11101
00110
01010
11110
00011
00101
01111
10001
10010
10111
Транспонируем, получаем цикл длины 5 из строк длины 15:
101011001000111
111101011001000
000111101011001
001000111101011
011001000111101. |
|
|
| номер сообщения: 49-25-3209 |
|
|
|
|
По-моему, Юрик, из тех замечательных фактов, что Вы установили выше, следует простая классификация деревьев.
Представим длину последовательности n в виде:
n = (2m+1)*2^p,
где m, p - неотрицательные целые.
Тогда из каждой точки цикла растет бинарное дерево T2^(2^p),
а в циклах лежат 2^(m*2^(p+1)) точек.
Т.е. с деревьями, вроде бы, разобрались.
Осталось понять, сколько есть циклов, и какие они. |
|
|
| номер сообщения: 49-25-3224 |
|
|
|
|
patrikey:
Тогда из каждой точки цикла растет бинарное дерево T2^(2^p),
а в циклах лежат 2^(m*2^(p+1)) точек. |
Да, это так. Не нашел в себе сил на формальное доказательство, но оно должно быть не безумно сложным.
Продолжая (после длительного перерыва, вызванного полным отсутствием прогресса) серию простых наблюдений:
мы установили дуальность между длинными циклами в коротких строках и короткими циклами в длинных строках. Задача нахождения цикла длины N в строках длины n эквивалентна нахождению непериодической строки длины N, лежащей в цикле длины n.
Пусть, например, мы задались вопросом, цикл какой максимальной длины существует в строках длины 5. Это то же самое, что спросить, какова максимальная длина периодa строки, удовлетворяющей соотношению
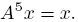
Его можно переписать, как
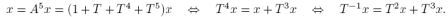
Отсюда следует, что любая подстрока длины 4 полностью определяет строку x (и вперед и назад), а, значит, строка обязательно будет периодической (без какого-либо предпериода) и период будет не больше 15 (число разных ненулевых подстрок длины 4). Пример такой строки был приведен выше: 000111101011001. Если присмотреться, то видно, что все подстроки длины 4 - разные, и пробегают по всем числам от 1 до 15 в двоичной записи.
Все это довольно легко обобщается на другие числа. Мы всегда получаен рекуррентное соотношение, гарантирующее, что любое решение будет периодическим. Дла простых случаев период находится без особого труда, например, для 9 получаем 63, для 17 - 255, а для 7 и 15 - 7 и 15. Но уже для 11 понять в лоб, почему нет строки с периодом 1023, а есть только строки с периодом 341 (этот факт мы в других терминах установили выше), у меня не получается. |
|
|
| номер сообщения: 49-25-3225 |
|
|
|
|
Какое место занимают вышеизложенные результаты в более широком математическом контексте, какова их ценность, с чем перекликаются/собачатся?  |
|
|
| номер сообщения: 49-25-3226 |
|
|
|
|
| номер сообщения: 49-25-3227 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2025 гг. |
|
|
|