|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Раз Пиррон отказывается - пишу решение :-)
Последние 4( а значит и 2-ой) в сумме набрали минимум 6 очков. Но 2-ой очевидно не мог набрать 6.5 или тем более 7, значит он - и последние 4 -набрал 6. Что значит, что последние проиграли все парти первым 4-м, в т. ч. и 7-ой 3-му. |
|
|
| номер сообщения: 49-2-780 |
|
|
|
|
Grigoriy: Раз Пиррон отказывается - пишу решение :-)
Последние 4( а значит и 2-ой) в сумме набрали минимум 6 очков. Но 2-ой очевидно не мог набрать 6.5 или тем более 7, значит он - и последние 4 -набрал 6. Что значит, что последние проиграли все парти первым 4-м, в т. ч. и 7-ой 3-му. |
Эх, я как раз двигался в правильном направлении... А все эти хваленые Квантринасы, Крысы, Хайдуки даже не рискнули хотя бы поискать решение. Вот так и выясняется горькая правда... |
|
|
| номер сообщения: 49-2-781 |
|
|
|
|
Grigoriy:
Последние 4 в сумме набрали минимум 6 очков. |
Откуда такая оценка?
| Grigoriy: Что значит, что последние проиграли все парти первым 4-м, в т. ч. и 7-ой 3-му. |
Почему??
Вот моя таблица турнира
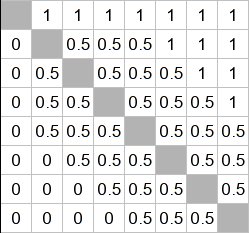
Условиям задачи вроде удовлетворяет. И где тут "последние проиграли все парти первым 4-м"? |
|
|
| номер сообщения: 49-2-782 |
|
|
|
|
MikhailK: Grigoriy:
Последние 4 в сумме набрали минимум 6 очков. |
Откуда такая оценка? |
Они играют 6 партий между собой. |
|
|
| номер сообщения: 49-2-783 |
|
|
|
|
MikhailK: Grigoriy:
Последние 4 в сумме набрали минимум 6 очков. |
Откуда такая оценка? |
А действительно - откуда такая оценка?!Ах, вот в чем дело - они ведь между собой играют... |
|
|
| номер сообщения: 49-2-784 |
|
|
|
|
iourique: MikhailK: Grigoriy:
Последние 4 в сумме набрали минимум 6 очков. |
Откуда такая оценка? |
Они играют 6 партий между собой. |
Спасибо, действительно. Мало я в круговиках играл. Уверен, что шахматисты такое сразу понимают, а мне думать приходится. |
|
|
| номер сообщения: 49-2-785 |
|
|
|
|
Мне удалось деформировать свою таблицу. В результате я получил уже две таблицы турнира
 
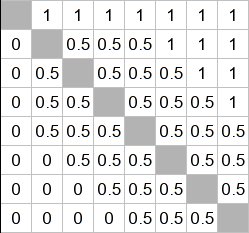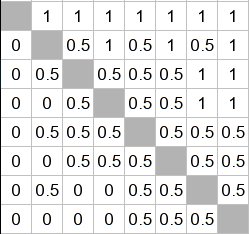
Обе таблицы вроде удовлетворяют условию задачи (проверьте!!).
Однако в первом турнире второй игрок выиграл у седьмого, а вот во втором сыграл вничью!
Grigoriy, где и кого дефект в рассуждениях? |
|
|
| номер сообщения: 49-2-786 |
|
|
|
|
| У Вас 2-ой не набирает 6 очков, только 4.5 |
|
|
| номер сообщения: 49-2-787 |
|
|
|
|
| Grigoriy: У Вас 2-ой не набирает 6 очков, только 4.5 |
На меня нашло затмение. Как выяснилось, я сегодня решал совсем другую задачу. Я сегодня утром ошибочно прочёл, что занявшие последние 4 места набрали в два раза больше очков, чем занявший 2-ое место. Произошло небольшое раздвоение двоек в исходной формулировке.  Я уж стирать свои посты не буду, но обращаю внимание, что к исходной задаче они не имеют никакого отношения. |
|
|
| номер сообщения: 49-2-788 |
|
|
|
|
| Забавная задачка. Доска размером 6*6 покрыта 18 костяшками домино размером 2*1 . Доказать, что можно разрезать доску по вертикали или горизонтали, не повредив ни одной доминошки. |
|
|
| номер сообщения: 49-2-1011 |
|
|
|
|
| Grigoriy: Забавная задачка. Доска размером 6*6 покрыта 18 костяшками домино размером 2*1 . Доказать, что можно разрезать доску по вертикали или горизонтали, не повредив ни одной доминошки. |
Доказывается от противного. Попробуем разложить домино так, чтобы доску нельзя было разрезать пилой по вертикали, не повредив ни одной костяшки. Чтобы пила не прошла между первым и вторым вертикальными рядами, по крайней мере 2 костяшки (из соображений чётности) должны лежать горизонтально. Аналогично, минимум 2 костяшки должны лежать горизонтально между 2-3, 3-4, 4-5, 5-6 вертикальными рядами - всего, чтобы преградить путь пиле, как минимум 10 горизонтальных костяшек.
Аналогично, чтобы пила не прошла между горизонтальными рядами, должно быть минимум 10 вертикально расположенных костяшек. 10+10=20, а у нас в паззле их всего 18... |
|
|
| номер сообщения: 49-2-1012 |
|
|
|
|
Изложение мне не нравится :-)
Цивилизованный(имхо) вариант:
Каждая линия разрезает чётное число костяшек(т к иначе с каждой стороны было бы нечётное число полей, что очевидно невозможно). Всего линий 10, если бы не было линий, не разрезающих ни одной костяшки, то получается минимум 20 костяшек, а их всего 18. |
|
|
| номер сообщения: 49-2-1013 |
|
|
|
|
Grigoriy: Очередная задачка :-) Дана окружность, на ней фиксированные точки А и В.
Точка М пробегает окружность. К - середина отрезка АМ. КР перпендикулярна ВМ (Р лежит на ВМ) Найти(описать) мн-во точек Р |
Задача похоже решается. Удалось получить очень простое уравнение кривой в полярных координатах с центром в точке B. К сожалению, выкладки я делал довольно небрежно и не следил за знаками и коэффицентами. Думаю , что как только отполирую решение, так сразу увижу ответ. |
|
|
| номер сообщения: 49-2-1014 |
|
|
|
|
| Доказать, что все прямые КР проходят через одну точку. Я опустил этот пункт, бывший в моём источнике, чтобы сделать задачу трудней и привлекательней для спецов из параллельного мира. |
|
|
| номер сообщения: 49-2-1015 |
|
|
|
|
| Grigoriy: Доказать, что все прямые КР проходят через одну точку. Я опустил этот пункт, бывший в моём источнике, чтобы сделать задачу трудней и привлекательней для спецов из параллельного мира. |
Ничего не понял. А тут не нужны трудные и привлекательные задачи? |
|
|
| номер сообщения: 49-2-1016 |
|
|
|
|
| :-) А разве я не помещаю? Но здесь я расчитываю скорее на уровень Пиррона. Эtа же задача даже в исходном виде - с предложением доказать существование общей точки - слишком технична и для меня, к примеру, представила сложности. В том же виде, в каком я её дал там - не думаю чтобы я решил, но это урoвень скажем Ваш, drowsy, NS |
|
|
| номер сообщения: 49-2-1017 |
|
|
|
|
| Grigoriy: Доказать, что все прямые КР проходят через одну точку. Я опустил этот пункт, бывший в моём источнике, чтобы сделать задачу трудней и привлекательней для спецов из параллельного мира. |
Для начала заметим, что после доказательства этого факта дальнейшее становится тривиальным. Назовём точку, через которую проходят все прямые KP, точкой R. Тогда RPB - прямоугольный треугольник c гипотенузой RB. Очевидно, что точка P всегда лежит на окружности, диаметром которой является отрезок RB.
Теперь займёмся доказательством того, что все прямые KP проходят через одну точку, и найдём её координаты. Я лично решал в лоб, алгебраически, в декартовых координатах. Для простоты возьмём единичную окружность, точку А с координатами (1, 0), точку B c координатами (Xb, Yb)=(Xb, sqrt(1-Xb^2)) и произвольную точку M с координатами (Xm, +-sqrt(1-Xm^2)). Далее ищется тангенс угла наклона прямой BM a(Xm), через него выражается наклон прямой KP a'(Xm)=-1/a(Xm) и находится офсет b'(Xm), при котором прямая проходит через точку K. Далее ищем точку X, в которой значение Y=X*a'+b' становится константой, не зависящей от Xm. Такая точка существует, её координаты ((1-Xb)/2, -Yb/2). Это и есть точка R, через которую проходят все прямые KP.
Теперь остаётся техническая задача нахождения параметров окружности, содержащей множество точек Р, по известным точкам B и R. Если я нигде не ошибся, центр её будет находиться в точке ((1+Xb)/4, Yb/4), а радиус будет равен sqrt(5/8-Xb*3/8).
Если бы я на месте Григория мучал бы этим вопросом студента, я бы ещё попросил его проверить знаки перед корнями в решении и показать, что любая точка на окружности принадлежит к множеству P (или найти подмножество точек P на окружности). |
|
|
| номер сообщения: 49-2-1019 |
|
|
|
|
| Grigoriy: Доказать, что все прямые КР проходят через одну точку. Я опустил этот пункт, бывший в моём источнике, чтобы сделать задачу трудней и привлекательней для спецов из параллельного мира. |
Это, по-моему, только с толку сбивает. Угол AMB постоянен. Если AN - перпендикуляр к MB, то P - середина MN. Отсюда сразу следует, что тангенс APB (APN) - это дважды тангенс AMB (AMN), и, следовательно, угол APB также постоянен. То бишь, P тоже заметает окружность. (Чуть-чуть возни еще нужно, чтобы показать, что дуги склеятся [tan b = 2*tan a -> tan(pi-b) = 2*tan(pi - a)].) |
|
|
| номер сообщения: 49-2-1020 |
|
|
|
|
| iourique: ...Угол AMB постоянен... |
Почему? |
|
|
| номер сообщения: 49-2-1021 |
|
|
|
|
Roger: | iourique: ...Угол AMB постоянен... |
Почему? |
Угол, опирающийся на дугу окружности, есть половина дуги. |
|
|
| номер сообщения: 49-2-1022 |
|
|
|
|
| Понял, тупой и острый угол Вы рассматриваете отдельно. |
|
|
| номер сообщения: 49-2-1023 |
|
|
|
|
| Roger: Понял, тупой и острый угол Вы рассматриваете отдельно. |
Ага, я там добавил комментарий втихую. Извиняюсь. |
|
|
| номер сообщения: 49-2-1024 |
|
|
|
|
| Да, Юрик показал, что и с пропущенным пунктом заддача не так страшна :-) Но несогласен, что он запутывает. Зная этот факт задача действительо становится тривиальной, а доказывается он легко. Понятно, что К описывает окружность - гомотетию исходной с центром гомотетии А и коэффициентом 1/2. А также очевидно лежит на этой окружности Продолжим КР через АМ в другую сторону и возьмём нa ней какую-нибудь точку Т. Тогда угол АКТ - постоянный(он дополнителен углу АМВ), т е все прямые КР (они же КТ) пересекают эту окружность в одной точке. |
|
|
| номер сообщения: 49-2-1025 |
|
|
|
|
Когда был помоложе, очень любил решать задачки, находясь в вагоне поезда, следующего из пункта А в пункт В.
Хочу предложить коллегам одну из таких задач, которую решал километров 500...
Задача чисто математическая, корректная, просто формулируется. Насколько вам покажется интересной и сложной - не знаю. Но, если справитесь, получите удовольствие...
Пуcть С(к) равно сумме цифр числа "два в степени "к"", записанного в десятичной системе счисления (то есть, обычной, так сказать). Доказать, что С(к) стремится к бесконечности при "к", стремящемся к бесконечности... |
|
|
| номер сообщения: 49-2-1214 |
|
|
|
|
Sad_Donkey: Когда был помоложе, очень любил решать задачки, находясь в вагоне поезда, следующего из пункта А в пункт В.
Хочу предложить коллегам одну из таких задач, которую решал километров 500...
Задача чисто математическая, корректная, просто формулируется. Насколько вам покажется интересной и сложной - не знаю. Но, если справитесь, получите удовольствие...
Путь С(к) равно сумме цифр числа "два в степени "к"", записанного в десятичной системе счисления (то есть, обычной, так сказать). Доказать, что С(к) стремится к бесконечности при "к", стремящемся к бесконечности... |
Красивая задачка, хотя, по-моему, не очень сложная. Если я все правильно посчитал, то есть такая оценка:
С(к) >= 1/3*(число знаков в записи 2^(к-1)). |
|
|
| номер сообщения: 49-2-1215 |
|
|
|
|
Простите, я не понял... Может кто-то поумнее меня выскажется...
Вот другая задача.
Каждое ребро тетраэдра является стороной двух треугольников - граней этого тетраэдра. Соответственно, к каждому ребру прилегают четыре угла, по два в каждом треугольнике.
Доказать, что у каждого тетраэдра есть ребро, для которого все прилегающие к нему углы - острые... |
|
|
| номер сообщения: 49-2-1216 |
|
|
|
|
| Sad_Donkey: Простите, я не понял... Может кто-то поумнее меня выскажется... |
Извиняюсь, проврался... |
|
|
| номер сообщения: 49-2-1217 |
|
|
|
|
iourique: | Sad_Donkey: Простите, я не понял... Может кто-то поумнее меня выскажется... |
Извиняюсь, проврался... |
Ну, что вы... Какие счеты... |
|
|
| номер сообщения: 49-2-1218 |
|
|
|
|
Sad_Donkey: Когда был помоложе, очень любил решать задачки, находясь в вагоне поезда, следующего из пункта А в пункт В.
Хочу предложить коллегам одну из таких задач, которую решал километров 500...
Задача чисто математическая, корректная, просто формулируется. Насколько вам покажется интересной и сложной - не знаю. Но, если справитесь, получите удовольствие...
Пуcть С(к) равно сумме цифр числа "два в степени "к"", записанного в десятичной системе счисления (то есть, обычной, так сказать). Доказать, что С(к) стремится к бесконечности при "к", стремящемся к бесконечности... |
Похоже, что я решил эту задачу с помощью цепных дробей.  Я умею сооружать такие степени двойки, которые имеют сколь угодно длинную последовательность девяток в начале. Отсюда немедленно следует решение задачи. |
|
|
| номер сообщения: 49-2-1221 |
|
|
|
|
MikhailK: Sad_Donkey: Когда был помоложе, очень любил решать задачки, находясь в вагоне поезда, следующего из пункта А в пункт В.
Хочу предложить коллегам одну из таких задач, которую решал километров 500...
Задача чисто математическая, корректная, просто формулируется. Насколько вам покажется интересной и сложной - не знаю. Но, если справитесь, получите удовольствие...
Пуcть С(к) равно сумме цифр числа "два в степени "к"", записанного в десятичной системе счисления (то есть, обычной, так сказать). Доказать, что С(к) стремится к бесконечности при "к", стремящемся к бесконечности... |
Похоже, что я решил эту задачу с помощью цепных дробей. Я умею сооружать такие степени двойки, которые имеют сколь угодно длинную последовательность девяток в начале. Отсюда немедленно следует решение задачи. |
Отсюда следует, что есть подпоследовательности, которые стремятся к бесконечности. Но доказывает ли это утверждение задачи? |
|
|
| номер сообщения: 49-2-1222 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|
