|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Оцените скорость мяча.
Фото скопировано с Ленты |
|
|
| номер сообщения: 49-2-3299 |
|
|
|
|
Любопытная задача с международной олимпиады:
 |
|
|
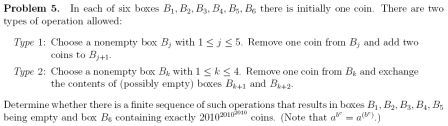| номер сообщения: 49-2-3300 |
|
|
|
|
Из игр с задачей Арнольда в параллельной ветке выросло несколько задачек. Может, сгодятся для какой-нибудь олимпиады школьников?
Некое число в бинарном представлении имеет n разрядов и состоит из одних единиц: 111...1.
Для какого n это число...
1)... делится на 3 ?
2)... делится на 5 ?
а можно объединить:
3)... делится на 15 ? |
|
|
| номер сообщения: 49-2-3317 |
|
|
|
|
patrikey: Из игр с задачей Арнольда в параллельной ветке выросло несколько задачек. Может, сгодятся для какой-нибудь олимпиады школьников?
Некое число в бинарном представлении имеет n разрядов и состоит из одних единиц: 111...1.
Для какого n это число...
1)... делится на 3 ?
2)... делится на 5 ?
а можно объединить:
3)... делится на 15 ? |
Для решения этой задачи достаточно выписать первые несколько чисел, тогда сразу видна закономерность. А зная уже ответ, не так уж сложно его обосновать.
У меня получилось, что из делимости на 5 автоматически следует делимость на 15. |
|
|
| номер сообщения: 49-2-3318 |
|
|
|
|
| номер сообщения: 49-2-3319 |
|
|
|
|
| MikhailK: Сложная задача, буквы слишком мелкие. |
Извиняюсь, действительно мелковато вышло.
Меня как-то потрясло, что совокупностью двух операций, одна из которых уменьшает число монет на 1,а другая - на 1 увеличивает, и обе уменьшают лексикографический порядок, можно всего из 6 монет получить совершенно астрономическое их число (в астрономии таких чисел, конечно, и в помине нет). |
|
|
| номер сообщения: 49-2-3320 |
|
|
|
|
| iourique: Меня как-то потрясло, что совокупностью двух операций, одна из которых уменьшает число монет на 1,а другая - на 1 увеличивает, и обе уменьшают лексикографический порядок, можно всего из 6 монет получить совершенно астрономическое их число (в астрономии таких чисел, конечно, и в помине нет). |
Аналогично. Я потренировался на четырёх кучках и подумал, что такого огромного количества монет достичь невозможно. |
|
|
| номер сообщения: 49-2-3321 |
|
|
|
|
| ...но стремиться к этому, - задача вполне достойная? |
|
|
| номер сообщения: 49-2-3322 |
|
|
|
|
| Roger: ...но стремиться к этому, - задача вполне достойная? |
Не вопрос! |
|
|
| номер сообщения: 49-2-3323 |
|
|
|
|
| MikhailK: такого огромного количества монет достичь невозможно. |
| Roger: ...но стремиться к этому, - задача вполне достойная? |
Ага, а потом искать среди них фальшивые. В этой теме много быстрых алгоритмов предлагали. |
|
|
| номер сообщения: 49-2-3324 |
|
|
|
|
MikhailK:
Для решения этой задачи достаточно выписать первые несколько чисел, тогда сразу видна закономерность. А зная уже ответ, не так уж сложно его обосновать.
У меня получилось, что из делимости на 5 автоматически следует делимость на 15. |
Да, действительно, все просто. Это как бы иллюстрация на тему: "математика - наука экспериментальная".
По поводу обоснования: я сначала все по мат. индукции делал; пока не заметил, что с геом.прогрессией все гораздо проще.
P.S. С трудом держусь, чтобы не щелкнуть по ссылке с монетами... |
|
|
| номер сообщения: 49-2-3329 |
|
|
|
|
В добавление к давно и долго обсуждавшейся задаче о шарах в мешке.
Мне предложили следующий вариант: пусть есть несколько человек, у каждого из которых есть целое число рублей. На каждом шаге мы случайно выбираем по очереди двух людей, и первый второму отдает один рубль. Люди, у которых деньги кончились, вылетают из игры. Игра заканчивается, когда все деньги оказываются у одного человека. В среднем сколько шагов будет в такой игре? |
|
|
| номер сообщения: 49-2-3379 |
|
|
|
|
| iourique: Игра заканчивается, когда все деньги оказываются у одного человека. В среднем сколько шагов будет в такой игре? |
Интересно, я подумаю.
PS Не знаю сколько будет шагов, но могу сказать точно, что все деньги окажутся у Абрамовича. |
|
|
| номер сообщения: 49-2-3381 |
|
|
|
|
iourique: В добавление к давно и долго обсуждавшейся задаче о шарах в мешке.
Мне предложили следующий вариант: пусть есть несколько человек, у каждого из которых есть целое число рублей. На каждом шаге мы случайно выбираем по очереди двух людей, и первый второму отдает один рубль. Люди, у которых деньги кончились, вылетают из игры. Игра заканчивается, когда все деньги оказываются у одного человека. В среднем сколько шагов будет в такой игре? |
На первый взгляд условие выхода из игры безденежных людей всё портит. У меня пока сходу не получается красиво записать это условие.
Кстати, у меня появилать забавная интерпретация этой игры. Пусть у нас N игроков. Количество рублей у игрока с номером n обозначим через x_n (n=1,2,...,N). Будем считать, что набор чисел x_n является координатами точки в N мерном пространстве. Эта точка в процессе игры всегда лежит на гиперплоскости x_1+x_2+...+x_N=Q, где Q - суммарное количество денег. Естественно, что все x_n также удовлетворяют условию 0 <= x_n <= Q (n=1,2,...,N).
Тогда весь процесс игры можно рассматривать как случайное блуждание по гиперплоскости x_1+x_2+...+x_N=Q. При этом условие выбывания безденежных людей сводится к условию "прилипания": если точка в процессе блуждания доходит до одной из координатных плоскостей (x_n=0, n=1,2,...,N), то она уже с этой плоскости не слезает. Так вот это условие "прилипания" и портит всю стройную картину. |
|
|
| номер сообщения: 49-2-3383 |
|
|
|
|
MikhailK:
Тогда весь процесс игры можно рассматривать как случайное блуждание по гиперплоскости x_1+x_2+...+x_N=Q. При этом условие выбывания безденежных людей сводится к условию "прилипания": если точка в процессе блуждания доходит до одной из координатных плоскостей (x_n=0, n=1,2,...,N), то она уже с этой плоскости не слезает. Так вот это условие "прилипания" и портит всю стройную картину. |
Красиво. |
|
|
| номер сообщения: 49-2-3386 |
|
|
|
|
| номер сообщения: 49-2-3436 |
|
|
|
|
Юрик, не могли бы привести оценку наибольшего числа перемещений/сдвигов книг, которые пришлось бы проделать библиотекарю в упрощённой задаче, когда, скажем, перемещать и ставить на своё место книгу можно лишь налево и значит сдвигать другие остаётся лишь направо  |
|
|
| номер сообщения: 49-2-3437 |
|
|
|
|
| Хайдук: Юрик, не могли бы привести оценку наибольшего числа перемещений/сдвигов книг, которые пришлось бы проделает библиотекарь в упрощённой задаче, когда, скажем, перемещать и ставить на своё место книгу можно лишь налево и значит сдвигать другие остаётся лишь направо |
2^{n-1}-1. |
|
|
| номер сообщения: 49-2-3438 |
|
|
|
|
Оценка эта с запасом или недалека от точной верхней границы? А само решение длинное? Я пытался, не очень напрягаясь, но ничего не вышло  |
|
|
| номер сообщения: 49-2-3440 |
|
|
|
|
| Хайдук: Оценка эта с запасом или недалека от точной верхней границы? А само решение длинное? Я пытался, не очень напрягаясь, но ничего не вышло |
Точный ответ. Решение несложное. |
|
|
| номер сообщения: 49-2-3441 |
|
|
|
|
iourique: | Хайдук: Оценка эта с запасом или недалека от точной верхней границы? А само решение длинное? Я пытался, не очень напрягаясь, но ничего не вышло |
Точный ответ. Решение несложное. |
Хайдук думает библиотекарем устроиться. Пытается оценить фронт работ. |
|
|
| номер сообщения: 49-2-3442 |
|
|
|
|
| iourique: Решение несложное. |
А почему тогда со сдвигами в оба направления сложнее? |
|
|
| номер сообщения: 49-2-3443 |
|
|
|
|
Хайдук: | iourique: Решение несложное. |
А почему тогда со сдвигами в оба направления сложнее? |
Оценка сверху не совпадает с оценкой снизу  . |
|
|
| номер сообщения: 49-2-3444 |
|
|
|
|
| MikhailK: Хайдук думает библиотекарем устроиться. Пытается оценить фронт работ. |
 |
|
|
| номер сообщения: 49-2-3445 |
|
|
|
|
Опубликую решение для простого случая. Сопоставим каждой перестановке книг сумму
Суммирование ведется по всем книгам, которые стоят на своем месте или левее (кроме самой последней), т.е. по тем книгам, которые нельзя двигать. У суммы есть три свойства: (1) ее минимальное значение - 0; (2) ее максимальное значение - 2^{n-1} - 1; (3) на каждом шаге она возрастает. Это дает оценку числа шагов сверху. Достижима ли она? Сумма равна 0, только если все книги (за исключением последней) стоят правее, чем нужно. Это возможно в одной единственной расстановке: n 1 2 3 ... n-2 n-1. Если на каждом шаге мы ставим на место книгу, стоящую на последнем месте, то полная расстановка как раз и займет 2^{n-1} - 1 шагов.
p.s. Есть и более лобовое доказательство по индукции. Оно основано на следующих соображениях: (1) как только мы поставим книгу 1 на место, задача сведется к предыдущей; (2) книгу, стоящую на первом месте нельзя двигать; (3) пока мы не двигаем книгу 1, мы можем мысленно поменять ее местами с книгой, стоящей на первом месте. Получается следующее: 2^{n-2} - 1 шагов (не трогаем книгу 1) + 1 шаг (ставим книгу 1 на место) + еще 2^{n-2} - 1 шагов (расставляем все остальное) = 2^{n-1} - 1 шагов. |
|
|
| номер сообщения: 49-2-3446 |
|
|
|
|
| пи(i) это функция из теории чисел или как? On top of my head не врубаюсь с чего взялись степени двойки? |
|
|
| номер сообщения: 49-2-3447 |
|
|
|
|
Есть веселая задачка, много разных версий. Идея в стиле что есть 3 кучки монет с разным количеством. На каждом шагу можно из большей кучки А в меньшую Б перекинуть некоторое количество монет, но так, чтобы число монет в Б увеличилось не более чем вдвое. Вопрос можно ли опустошить одну из кучек.
Подсказка - можно  . Главное показать стратегию как это делать. Это само по себе уже не просто. Но самое интересное после этого - я немного попарился пытаясь дать какой-то лимит минимальному количество шагов. Я так понимаю, что ни у кого ответа на это нет, а задачка любопытная.
__________________________
ИМХО |
|
|
| номер сообщения: 49-2-3448 |
|
|
|
|
Юрик, а как быть с тремя (n = 3) книгами в этом непорядке, 312 ? В худшем случае упорядочиваем следующим образом:
321 - книгу 2 поставили на её место, а книгу 1 сдвинули вправо, сделали 2 хода
132 - книгу 1 поставили на её место, а книги 3 и 2 сдвинули вправо, сделали 3 хода
123 - книгу 2 поставили на её место, а книгу 3 сдвинули вправо, сделали 2 хода
В общем сделали 7 ходов, то бишь индивидуальных операций с книгами, что вяжется с формулой 2^n - 1, а не с 2^(n-1) - 1
 |
|
|
| номер сообщения: 49-2-3449 |
|
|
|
|
А вот с четырмя (n = 4) книгами в таком непорядке, 4123. В худшем случае упорядочиваем следующим образом:
4123 - начальная позиция
4213 - книгу 2 поставили на место, а книгу 1 сдвинули вправо, 2 хода
4231 - книгу 3 поставили на место, а книгу 1 сдвинули вправо, 2 хода
1423 - книгу 1 поставили на место, а книги 4, 2 и 3 сдвинули вправо, 4 хода
1432 - книгу 3 поставили на место, а книгу 2 сдвинули вправо, 2 хода
1243 - книгу 2 поставили на место, а книги 4 и 3 сдвинули вправо, 3 хода
1234 - книгу 3 поставили на место, а книгу 4 сдвинули вправо, 2 хода
В общем сделали 2^4 - 1 = 15 ходов. |
|
|
| номер сообщения: 49-2-3450 |
|
|
|
|
А вот что происходит с упорядочиванием 4132:
4132 - начальная позиция
4213 - книгу 2 поставили на место, а книги 1 и 3 сдвинули вправо, 3 хода
4231 - книгу 3 поставили на место, а книгу 1 сдвинули вправо, 2 хода
1423 - книгу 1 поставили на место, а книги 4, 2 и 3 сдвинули вправо, 4 хода
1432 - книгу 3 поставили на место, а книгу 2 сдвинули вправо, 2 хода
1243 - книгу 2 поставили на место, а книги 4 и 3 сдвинули вправо, 3 хода
1234 - книгу 3 поставили на место, а книгу 4 сдвинули вправо, 2 хода
Зделали 2^4 = 16 ходов |
|
|
| номер сообщения: 49-2-3451 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2025 гг. |
|
|
|
