|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Ниже приведена ссылка на статью с решением задачи о трёх шляпах
The Three Hat Problem
Brian Benson, Yang Wang
| In this paper we study the Three Hat Problem which appeared in Puzzle Corner of the Technology Review magazine. This puzzle gives a scenario in which three players wearing hats are sitting together and each hat can be seen by everyone except the player that is wearing that hat. Each player is told that all of the hats contain a positive integer and that two of the integers add to the third. In an ordered, turn-wise, modular fashion, each player truthfully states whether or not he knows his integer. We give a strategy which allows for one of the players to solve for his integer for all possible integer configurations of the puzzle and prove it is the optimal such strategy. |
|
|
|
| номер сообщения: 49-2-221 |
|
|
|
|
ivаnk: Jeweller: положим немного сахара под язык. Что мы чувствуем, тепло или холодок? Вывод: похоже  , что реакция эндотермическая.
|
Смайлик Вы не зря поставили  , так как неизвестно еще, что Вы почувствуете и по какой причине. |
Да, поэтому смайлик и поставил. 
Ясно помню, что много лет назад, когда проверял, чувствовал холодок. А вчера, по случаю футбольной победы немного  , решил проверить, так вообще ничего не почувствовал. Перепроверил – результат тот же.
ivаnk: | Jeweller: ivаnk, мы мыслим одинаково, но с противоположных сторон. Вам больше по душе замерзание, мне – кипение. |
При растворении сахара температура кипения раствора будет повышаться, поэтому... |
Тоже об этом подумал. Лучше Ваша модель с двумя емкостями. Во внутренней растворяем сахар, внешняя вскипает.
Но Ваша идея с конденсатом изящнее. Мне понравилась!
Когда ее прочитал, придумал кажется универсальный способ. Все как у Вас, только вместо герметичной емкости берем воздушный шарик с равновесием пар-жидкость внутри! Привязываем его ко дну емкости, заливаем полностью водой, отмечаем уровень воды в емкости. И начинаем растворять сахар!
Если реакция эндотермическая, давление внутри шарика и его объем будут уменьшаться, уровень воды в емкости понизится.
Если реакция экзотермическая – соответственно наоборот и уровень воды повысится.
Чем больше долевой объем шарика в системе шарик – вода, тем система чувствительнее. |
|
|
| номер сообщения: 49-2-224 |
|
|
|
|
MikhailK: Ниже приведена ссылка на статью с решением задачи о трёх шляпах
|
Я тогда, не читая статьи, расскажу свое решение, а потом можно будет сравнить  .
1. Будем искать случаи, когда игра короткая, начиная с самых коротких. Это полезно для понимания, т.к такие случаи, наверное, окажутся самыми простыми. А кроме того, один из коротких случаев может совпасть с первой серией, ведь она тоже короткая (по сравнению со второй).
2. По условию, число любого мудреца является либо суммой, либо разницей чисел его соседей. Поэтому мудрецы могут рассуждать "от противного". Простейший (наиболее "информативный") случай, когда мудрец может определить свое число - это когда у обоих его соседей одинаковое число (n). Тогда его число не может быть разницей, а только суммой, т.е равняться 2n.
3. Тогда следующий по информативности случай - это когда числа мудрецов представляют собой множество {n, 2n, 3n}. Этот случай весьма информативен, т.к. может сводиться к простейшему (в ходе рассуждений мудрецов от противного) в целых двух ситуациях: 2n-n=n и 3n-2n=n.
4. Для множества {n, 2n, 3n} возможно 6 перестановок, для каждой нужно рассчитать сценарий игры.
5. Возьмем, например, перестановку (A,B,C)=(2n,n,3n).
Во время каждого шага отвечающий мудрец рассматривает две возможности, чему равно его число (сумма или разность) и на основании известных ему запретов делает вывод.
1-й шаг. A - может только сделать тривиальный вывод, что числа его соседей не равны, поэтому говорит "не знаю". Зато его соседи узнают каждый по запрету: B узнает, что B><3n, а С узнает, что C><n.
2-й шаг. B понимает, что B=5n либо B=n. Но запретов на эти числа у него нет, поэтому он говорит "не знаю".
3-й шаг. C понимает, что С=3n либо С=n. Но на C=n ему известен запрет, поэтому он делает вывод, что С=3n и заканчивает игру.
6. Аналогично рассмотрев все шесть перестановок, можно увидеть что в одном случае игра прерывается на B в "первом круге" (обозначим это как B1), в двух случаях - на С1 и в одном случае - на B2. В двух случаях игра прерывается, как нам вроде бы и нужно, на A2. Но в обоих этих случаях A=3n, а ведь 50 не делится на 3. Так что решением должна быть какая-то из оставшихся четырех перестановок. Такое возможно только в том случае, если мудрец A (и все остальные мудрецы) использует какие-то дополнительные рассуждения. Наверное, это рассуждения от противного.
7. Рассмотрев с этой точки зрения четыре перестановки, можно сделать вывод (тут я сокращаю), что мудрец A может использовать только те случаи, в которых происходит остановка C1. А именно, в искомой ситуации он поймет, что A не может быть разностью, т.к. тогда произошла бы остановка С1.
8. Рассмотрим тогда случаи C1 (тут я тоже сокращаю).
A=2n, B=n, C=3n Мудрец A понимает, что А должна быть суммой, т.е A=4n. Нам этот случай не подходит, т.к 50 не делится на 4.
A=n, B=2n, C=3nА вот этот случай подходит, т.к A=5n, а 50 делится на 5.
Таким образом, n=50/5=10, B=2n=20, С=3n=30.
Это решение не гарантирует единственность. |
|
|
| номер сообщения: 49-2-225 |
|
|
|
|
Jeweller:
Когда ее прочитал, придумал кажется универсальный способ. Все как у Вас, только вместо герметичной емкости берем воздушный шарик с равновесием пар-жидкость внутри! Привязываем его ко дну емкости, заливаем полностью водой, отмечаем уровень воды в емкости. И начинаем растворять сахар!
Если реакция эндотермическая, давление внутри шарика и его объем будут уменьшаться, уровень воды в емкости понизится.
Если реакция экзотермическая – соответственно наоборот и уровень воды повысится.
Чем больше долевой объем шарика в системе шарик – вода, тем система чувствительнее. |
Красота! Я предложу всю это историю знакомому, который учит школьников экспериментальной физике. Школьники выбирают тему из списка (обычно одну на двоих), придумывают и проводят эксперимент, (используя обычно простейшие подручные средства), а затем докладывают результаты на школьной конференции. Там как раз темы вроде нашей: «Измерение атмосферного давления без барометра», «Определение скорости теплового движения молекул», «От чего и как зависит сила сопротивления при движении тела в жидкости» и так далее. |
|
|
| номер сообщения: 49-2-226 |
|
|
|
|
| Надо признать, что я ничего не понял, но основная идея понятна. В выходные поплотнее поразмышляю над задачкой. |
|
|
| номер сообщения: 49-2-227 |
|
|
|
|
Эх, нашел ошибку в своей модели.
Надо ведь еще учитывать изменение уровня раствора в емкости при добавлении сахара. Объем расплавленного сахара ~ 0.6 объема кристаллического сахара. Т.е. для чистоты эксперимента нужно при добавлении единицы объема сахара изъять 0.6 единицы объема воды.
Сделать это можно так, исходя из того, что отношение 0.6 нам заранее не известно. Берем небольшую емкость с тонкими стенками. Заполняем ее полностью сильно концентрированным раствором сахара, на приготовление которого ушел объем Х сахара и объем Y воды. Такие же объем Х сахара и объем Y воды отмеряем и оставляем пока в сторонке, естественно не смешанные! Закупориваем емкость, опускаем в емкость с водой, замеряем уровень. Дальше вынимает емкость с раствором, вносим объем Х сахара и объем Y воды, размешиваем сахар. Все, поправку на объем сахара сделали.
Или, еще проще. Берем ту же маленькую герметичную емкость с хорошо теплопроводящими стенками, но пустую. Опускаем ее в воду (на грузике, например), отмечаем уровень. Вынимаем, загружаем сахаром и водой, закупориваем, опускаем и начинаем ее легонько крутить вокруг своей оси! Дальше понятно.
Да, усложнение – враг изящества!
Нет, подождите! Мы же можем сразу положить сахар внутрь воздушного шарика, закрепив его на стенке так, чтобы он не соприкасался с водой внутри шарика, т.е. сахар уже там  , ничего добавлять не надо! Замеряем уровень, щелчком отцепляем сахар и начинаем легонько крутить шарик вокруг своей оси!
Теперь все, кажется.
|
|
|
| номер сообщения: 49-2-228 |
|
|
|
|
Jeweller: вместо герметичной емкости берем воздушный шарик с равновесием пар-жидкость внутри! Привязываем его ко дну емкости, заливаем полностью водой, отмечаем уровень воды в емкости. И начинаем растворять сахар!
Если реакция эндотермическая, давление внутри шарика и его объем будут уменьшаться, уровень воды в емкости понизится.
Если реакция экзотермическая – соответственно наоборот и уровень воды повысится.
Чем больше долевой объем шарика в системе шарик – вода, тем система чувствительнее. |
Я правильно понимаю, что в шарике именно пар-вода (а не просто воздух), чтобы увеличить чувствительность системы? Так как при понижении температуры объем будет падать не только за счет уменьшения температуры, но и за счет уменьшения числа молекул в газообразной фазе (из-за конденсации).
Jeweller:
Нет, подождите! Мы же можем сразу положить сахар внутрь воздушного шарика, закрепив его на стенке так, чтобы он не соприкасался с водой внутри шарика, т.е. сахар уже там , ничего добавлять не надо! Замеряем уровень, щелчком отцепляем сахар и начинаем легонько крутить шарик вокруг своей оси!
|
Тогда появляется другой артефакт: растворение сахара (или другого вещества) в системе пар-жидкость уже само по себе сдвигает равновесие. Т.к. сахар нелетуч, то интуитивно равновесие будет сдвигаться в сторону жидкости. |
|
|
| номер сообщения: 49-2-229 |
|
|
|
|
ivаnk:
Я правильно понимаю, что в шарике именно пар-вода (а не просто воздух), чтобы увеличить чувствительность системы? Так как при понижении температуры объем будет падать не только за счет уменьшения температуры, но и за счет уменьшения числа молекул в газообразной фазе (из-за конденсации). |
Да, это и имел в виду.
Вообще, если найти жидкость, более чувствительную к изменению температуры около значения Тэксперимента, лучше использовать ее внутри воздушного шарика для дальнейшего увеличения чувствительности системы в целом. Скажем, вещество, чья Ткипения близка к Тэксперимента.
Для Вашей модели с конденсатом на стенках колбы тоже лучше. Кажется, Ваша модель с конденсатом становится универсальной.
1. Используем вещество в колбе, чья Ткипения только чуть ниже Тэксперимента. Вещество в колбе кипит. Если реакция эндотермическая, вещество в колбе перестанет кипеть.
2. Используем вещество в колбе, чья Ткипения только чуть выше Тэксперимента. Вещество в колбе не кипит. Если реакция экзотермическая, вещество в колбе начнет кипеть.
Или, другой вариант: не меняем вещество в колбе, а меняем Тэксперимента вокруг Ткипения вещества в колбе.
ivаnk:
Jeweller:
Нет, подождите! Мы же можем сразу положить сахар внутрь воздушного шарика, закрепив его на стенке так, чтобы он не соприкасался с водой внутри шарика, т.е. сахар уже там , ничего добавлять не надо! Замеряем уровень, щелчком отцепляем сахар и начинаем легонько крутить шарик вокруг своей оси!
|
Тогда появляется другой артефакт: растворение сахара (или другого вещества) в системе пар-жидкость уже само по себе сдвигает равновесие. Т.к. сахар нелетуч, то интуитивно равновесие будет сдвигаться в сторону жидкости. |
Да, об этом я не подумал. Мы ведь заранее не знаем.
И, кроме того, тут есть еще одна дырка. Хоть сахар уже там, и ничего добавлять не надо, когда он раствориться, его объем уменьшится на ~40% и надо компенсировать, добавив соответствующий объем воды. В основную емкость.
Похоже, лучше ничего внутрь шарика или колбы не добавлять. |
|
|
| номер сообщения: 49-2-231 |
|
|
|
|
Jeweller:
Для Вашей модели с конденсатом на стенках колбы тоже лучше. Кажется, Ваша модель с конденсатом становится универсальной.
1. Используем вещество в колбе, чья Ткипения только чуть ниже Тэксперимента. Вещество в колбе кипит. Если реакция эндотермическая, вещество в колбе перестанет кипеть.
2. Используем вещество в колбе, чья Ткипения только чуть выше Тэксперимента. Вещество в колбе не кипит. Если реакция экзотермическая, вещество в колбе начнет кипеть.
Или, другой вариант: не меняем вещество в колбе, а меняем Тэксперимента вокруг Ткипения вещества в колбе.
|
Согласен, но это уже не похоже на бытовые условия . |
|
|
| номер сообщения: 49-2-233 |
|
|
|
|
ivаnk:
Согласен, но это уже не похоже на бытовые условия . |
В бытовых условиях не реализуемо.
Сегодня мне приснились «чудо-резиночка», «чудо-проволочка» и «чудесный гелиевый шарик». Первые две идеи фантастические, третья – «сумасшедшая».
Кажется, пора завязывать со всем этим, пока не поздно!
1. «Чудо-резиночка».
Идея заключается в изменении положения грузика, подвешенного на длинной «чудо-резиночке», чья эластичность очень чувствительна к изменению температуры. Резиночка сверху жестко закреплена и находится вместе с грузиком внутри емкости с водой. Сахар растворяем покручиванием в хорошо теплопроводящей герметичной колбе с минимумом воздуха, помещенной целиком в емкость с водой. (В отдельной колбе, чтобы исключить изменение положения грузика из-за изменения значения выталкивающей силы на него в связи с изменением плотности воды при растворении сахара в основной емкости.)
2. «Чудо-проволочка».
Идея заключается в изменении положения грузика, прикрепленного к концу горизонтально расположенной длинной упругой «чудо-проволочки», чья характеристика на прогиб очень чувствительна к изменению температуры. Проволочка с грузиком внутри емкости с водой. Сахар растворяем также, как в модели с «Чудо-резиночкой».
3. «Чудесный гелиевый шарик».
Изготавливаем жесткий «чудесный гелиевый шарик» постоянного объема с малой теплопроводностью стенок, такой, что бы он был подвешен, «свободно парил» внутри колбы (с хорошей теплопроводностью стенок), в которой установилось равновесие пар-вода. Закупориваем колбу, закрепляем ее внутри емкости с водой, начинаем растворять сахар в основной емкости. В зависимости от того, эндо- или экзо- реакция, наблюдаем, как при эндо-реакции – температура и давление внутри колбы уменьшаются, образуется конденсат, в более разреженной среде подъемная сила уменьшается, и более теплый! «чудесный гелиевый шарик» опускается вниз колбы, при экзо-реакции – наоборот, поднимается вверх!
Вместо «чудесного гелиевого шарика» можно использовать его родственника – «чудесный вакуумный шарик».
Теперь две здравые идеи с хорошим визуальным эффектом. Для их реализации нам потребуется ввести в эксперимент второй «эталонный раствор».
В емкости с объемом воды X растворяем объем Y сахара. Ждем, когда установится термодинамическое равновесие, Траствора станет равна комнатной. Это и будет нашим «эталонным раствором».
4. «Чайная каракатица».
Подкрашивает «эталонный раствор», положив в него чайных листьев. Пренебрегаем крайне незначительным изменением плотности «эталонного раствора» при подкрашивание чайными листьями. Изготавливаем «каракатицу» - инструмент для забора и впрыска подкрашенного «эталонного раствора» - например, берем вертикальную полую трубку, изогнутую снизу горизонтально, сверху резиновая груша.
Во второй, экспериментальной, теплоизолированной емкости с объемом воды X, находящейся при комнатной температуре, растворяем объем Y сахара. Даем раствору «успокоиться». Набираем чайный «эталонный раствор» в «каракатицу» и перенеся ее в экспериментальную емкость так, чтобы горизонтальное «сопло» было на половине глубины, выпускаем с помощью груши подкрашенный «эталонный раствор». Смотрим, куда он начнет больше перемещаться, вверх или вниз. Если вверх – эндотермическая реакция, вниз – экзотермическая.
Диффузия особо не помешает, важна относительная вертикальная динамика.
Действуем исходя из того, что растворение некоторого количества сахара в емкости с водой незначительно изменяет температуру максимальной плотности раствора относительно температуры максимальной плотности воды = 4С, во всяком случае, что температура максимальной плотности раствора меньше комнатной.
5. «Равновесный воздушный шарик».
Надуваем воздушный шарик воздухом комнатной температуры, подвязываем к нему грузик, и аккуратно подбираем массу грузика так, чтобы шарик свободно плавал – «парил» в емкости с «эталонным раствором» (сила тяжести = выталкивающей силе). Это будет наш «равновесный воздушный шарик».
Во второй, экспериментальной, теплоизолированной емкости с объемом воды X, находящейся при комнатной температуре, растворяем объем Y сахара. Даем раствору «успокоиться». Опускаем в него «равновесный воздушный шарик».
Если реакция эндотермическая, сначала шарик будет наверху – плотность раствора чуть увеличилась, выталкивающая сила, действующая на теплый раздутый шарик, больше силы тяжести. По мере достижения равновесия между шариком и раствором, температура и объем шарика начнут уменьшаться, и мне кажется (тут я могу ошибаться), что при другой температуре раствора, в общем случае, он может и не стать «равновесным воздушным шариком», даже опуститься на дно, до момента достижения в системе комнатной температуры, конечно, когда он снова станет «равновесным воздушным шариком». Но для ответа на наш вопрос достаточно того, что сначала он будет наверху.
Если реакция экзотермическая – все наоборот, сначала шарик опуститься вниз. |
|
|
| номер сообщения: 49-2-240 |
|
|
|
|
Мдя... А я про мудрецов знаю только, что они в одном тазу пустились по морю в грозу. А на них, оказывается, еще и щляпы были...
__________________________
Спасение там, где опасность. |
|
|
| номер сообщения: 49-2-242 |
|
|
|
|
"Здравые" идеи не сразу понял, но потом они мне понравились. История с сахаром становится все поучительнее: более очевидные идеи (три "чудо"-идеи) с точки зрения реализации уступают менее очевидным ("здравые" идеи).
Jeweller:
Кажется, пора завязывать со всем этим, пока не поздно!
|
Согласен . У меня, по-видимому, сработали какие-то механизмы самосохранения - я почти неделю проболел |
|
|
| номер сообщения: 49-2-261 |
|
|
|
|
ivаnk, выздоравливайте полностью.
Пейте чай с сахаром (и с малиной), да погорячее.
В моем случае механизм самосохранения сработал у компа. Как только устраню все неполадки, выложу результат «кухонного» эксперимента и модель «Диафрагма» (в продвинутом варианте «Капилляр») – она самая чувствительная из всех предложенных и с хорошим (для «Капилляра» - лучшим) визуальным эффектом. |
|
|
| номер сообщения: 49-2-262 |
|
|
|
|
| номер сообщения: 49-2-263 |
|
|
|
|
Прочитал статью про шляпы. Сравнение с моим "решением" было очень поучительным. 
MikhailK, спасибо за задачи со статьями. Они выводят на какие-то более серьезные вопросы, это хороший стиль. |
|
|
| номер сообщения: 49-2-282 |
|
|
|
|
ivаnk: Прочитал статью про шляпы. Сравнение с моим "решением" было очень поучительным.
MikhailK, спасибо за задачи со статьями. Они выводят на какие-то более серьезные вопросы, это хороший стиль. |
А я воспользовался правом задающего и задачу не решил и даже практически не думал.  Обещал подумать в выходные, но как-то не получилось. |
|
|
| номер сообщения: 49-2-283 |
|
|
|
|
Кстати, Jeweller, я так и не понял, чем все кончилось. Кроме дискуссии о типе реакции, там есть еще ньюансы? |
|
|
| номер сообщения: 49-2-290 |
|
|
|
|
jenya:
Кстати, Jeweller, я так и не понял, чем все кончилось. Кроме дискуссии о типе реакции, там есть еще ньюансы? |
Я просто боюсь лишний раз писать в этой теме.
Все, конечно началось со статуи Менделеева-Ломоносова в соседней теме. Я там что-то не то сказал видимо, даже знаю что. Но тогда начались просто неполадки с операционкой. Здесь же, в этой теме, почти каждый пост сопровождается, сопровождается пост...
Вообщем, сейчас я без двух сидиромов, без флопика, с половиной сгоревших проводов, с которых стекла (т.к. горела ) изоляция, с полусгоревшим блоком питания, который вообще непонятно как еще работает.
Поэтому хотел подвести итог и выложить результат маленького эксперимента (который еще не провел) и итоговую модель одновременно.
Однако, не ответить Вам, jenya, я не могу! Рискнем.
Дополнительных ньюансов по физике процесса нет, есть момент выхода из пассивного выбора одного из данных первоначальных вариантов ответа к активному их расширению после прояснения ситуации.
Вопрос:
Утром Вы заварили чай и тут вспомнили, что нужно сделать срочный телефонный звонок. Вы хотите, чтобы по его окончании, чай остыл как можно меньше. Как лучше поступить:
1. Растворить сахар до телефонного разговора.
2. Растворить сахар после телефонного разговора.
3. Не имеет значения. |
преподаватель задал после окончания пары трем задержавшимся студентам, в числе которых случайно оказался и я, просто для того, чтобы еще пару-тройку минут пообщаться и проститься с хорошим настроением. И это ему вполне удалось!
После «вскрытия» вопроса, «открытия» «так называемой субъективной» и «так называемой объективной» проверки на эндо- экзо- термичность и выбора 1-го варианта ответа, пристально ожидающий и чуть ироничный взгляд преподавателя нас явно не отпускал, пока кто-то не сказал: «А еще лучше,.. да, еще лучше пить чай без сахара!»
Эхо от нашего смеха еще долго бродило по опустевшей аудитории...
Однако, и того ответа, что дали Вы, jenya, вполне достаточно.
Вопрос можно считать закрытым.
«Пытаясь найти решение, мы можем многократно менять свою точку зрения, свой взгляд на задачу. Мы принуждены менять свою позицию вновь и вновь. Весьма вероятно, что наше представление о задаче в значительной степени неполно, когда мы начинаем работу; наша точка зрения становится иной, когда сделаны некоторые успехи; она вновь меняется к тому моменту, когда решение почти в наших руках.»
Д. Пойа |
|
|
|
| номер сообщения: 49-2-292 |
|
|
|
|
| Jeweller: «А еще лучше,.. да, еще лучше пить чай без сахара!» |
В свое время Чич предлагал другое (кардинальное) решение проблемы остывания чая. |
|
|
| номер сообщения: 49-2-293 |
|
|
|
|
Пора поднимать тему. Я немного пришёл в себя после одновременного написания двух статей.
Пару дней назад один мой знакомый рассказал вот такую задачу.
Задача о сетке сопротивлений. Имеется бесконечная плоская сетка с квадратными ячейками. Сопротивление каждой стороны ее ячейки равно 1 Ом. Найти сопротивление сетки между ближайшими её узлами.
Задача знакомая и вроде имеет красивое решение, но я не смог его найти. Вместо этого я вывел общую формулу для сопротивления между двумя произвольными узлами сетки. Получилась красивая формула, содержащая функции Бесселя мнимого аргумента. Упростить её мне пока не удалось.
Забавно, что численное вычисление по моей формуле даёт очень простой ответ в случае ближайших узлов. Пошёл искать подходящие свойства бесселей. |
|
|
| номер сообщения: 49-2-350 |
|
|
|
|
MikhailK:
Задача о сетке сопротивлений. Имеется бесконечная плоская сетка с квадратными ячейками. Сопротивление каждой стороны ее ячейки равно 1 Ом. Найти сопротивление сетки между ближайшими её узлами.
|
Помню такую задачу, ответ вроде 0.5 Ома.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-351 |
|
|
|
|
Quantrinas: MikhailK:
Задача о сетке сопротивлений. Имеется бесконечная плоская сетка с квадратными ячейками. Сопротивление каждой стороны ее ячейки равно 1 Ом. Найти сопротивление сетки между ближайшими её узлами.
|
Помню такую задачу, ответ вроде 0.5 Ома.
|
К меня получается 0.25, но я запросто мог где-то потерять двойку. Мне интересно узнать простое решение задачки. Так же любопытно, а есть ли простая общая формула. |
|
|
| номер сообщения: 49-2-352 |
|
|
|
|
MikhailK:
К меня получается 0.25, но я запросто мог где-то потерять двойку. Мне интересно узнать простое решение задачки. |
Точно не помню, давно было.
Примерно так: в один узел втекает ток I и растекается равномерно на бесконечность, из соседнего узла ток I вытекает "собираясь" с бесконечности. Между узлами течёт 0.25I+0.25I=0.5I, напряжение 0.5I * 1 Ом, соответственно сопротивление 0.5 Ом. Может наврал что.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-353 |
|
|
|
|
Quantrinas: MikhailK:
К меня получается 0.25, но я запросто мог где-то потерять двойку. Мне интересно узнать простое решение задачки. |
Точно не помню, давно было.
Примерно так: в один узел втекает ток I и растекается равномерно на бесконечность, из соседнего узла ток I вытекает \\\"собираясь\\\" с бесконечности. Между узлами течёт 0.25I+0.25I=0.5I, напряжение 0.5I * 1 Ом, соответственно сопротивление 0.5 Ом. Может наврал что.
|
Всё верно, спасибо. Я нашёл у себя ошибку. Вот мой общий ответ для сопротивления между узлом (0,0) и (i,j)
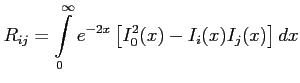
Судя по твоему решению, этот ответ можно упростить |
|
|
| номер сообщения: 49-2-354 |
|
|
|
|
MikhailK: Вот мой общий ответ для сопротивления между узлом (0,0) и (i,j)
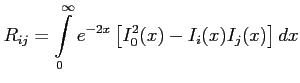
Судя по твоему решению, этот ответ можно упростить |
Охренеть. Я и не думал, что это так сложно, Бесселя, да ещё модифицированные, жуть.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-355 |
|
|
|
|
К задаче о сетке сопротивлений
Простое изложение можно посмотреть тут
Infinite 2D square grid of resistors
Рекомендую вот эту статью. Mне очень понравилось, особенно таблица 1.
D. Atkinson and F. J. van Steenwijk
Infinite resistive lattices
American Journal of Physics, vol. 67, 486 (1999)
| The resistance between two arbitrary nodes in an infinite square lattice of identical resistors is calculated. The method is generalized to infinite triangular and hexagonal lattices in two dimensions, and also to infinite cubic and hypercubic lattices in three and more dimensions. |
Jozsef Cserti, Gyula David, Attila Piroth
Perturbation of infinite networks of resistors
Am. J. Phys. 70, 153 (2002)
| Abstract.The resistance between arbitrary nodes of an infinite network of resistors is calculated when the network is perturbed by removing one bond from the perfect lattice. A relation is given between the resistance and the lattice Green's function of the perturbed resistor network. By solving the Dyson equation, the Green's function and the resistance of the perturbed lattice are expressed in terms of those of the perfect lattice. Numerical results are presented for a square lattice. |
Вот, например, какое значение приведено в этой статье для сопротивления между точками (0,0) и (50,50) квадратной сетки сопротивлений (нужно кликнуть на мусор внизу, чтобы посмотреть полноразмерную картинку)
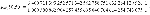
Jozsef Cserti
Application of the lattice Green's function for calculating the resistance of an infinite network of resistors
Am. J. Phys. 68, 896 (2000)
| Abstract.The resistance between two arbitrary grid points of several infinite lattice structures of resistors is calculated by using lattice Green's functions. The resistance for d dimensional hypercubic, rectangular, triangular, and honeycomb lattices of resistors is discussed in detail. Recurrence formulas for the resistance between arbitrary lattice points of the square lattice are given. For large separation between nodes the asymptotic form of the resistance for a square lattice and the finite limiting value of the resistance for a simple cubic lattice are calculated. The relation between the resistance of the lattice and the van Hove singularity of the tight-binding Hamiltonian is given. The Green's function method used in this paper can be applied in a straightforward manner to other types of lattice structures and can be useful didactically for introducing many concepts used in condensed matter physics. |
Добавлю ещё ссылочку на свежую работу
J.H. Asad, A. Sakaji, R.S. Hijjawi, and J.M. Khalifeh
On the resistance of an infinite square network of identical resistors - Theoretical and experimental comparison
Eur. Phys. J. B, vol. 52, (2006).
| Abstract. A review of the theoretical approach for calculating the resistance between two arbitrary lattice points in an infinite square lattice (perfect and perturbed cases) is carried out using the lattice Green's function. We show how to calculate the resistance between the origin and any other site using the lattice Green's function at the origin, Go(0, 0), and its derivatives. Experimental results are obtained for a finite square network consisting of 30x30 identical resistors, and a comparison with those obtained theoretically is presented. |
В этой статье приведены любопытные рекуррентные соотношения.
К сожалению копию этой статьи в свободном доступе мне пока найти не удалось.
Мне задачка понравилась. Особенно впечатляет, что на эту тему до сих пор пишутся интересные и содержательные статьи.
PS Мой ответ с функциями Бесселя оказался правильным, однако в статьях выше используется другое, более удобное при вычислениях, выражение, которое однако является несимметричным относительно i и j. |
|
|
| номер сообщения: 49-2-356 |
|
|
|
|
Не там искал!!!
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-388 |
|
|
|
|
Обалдеть. Я похоже нашёл решение задачи, которая меня давно интересовала.
Начну постепенно. Ещё в школе проходят, что длины сторон треугольника должны удовлетворять трём условиям: a<b+c, b<a+c, c<a+b. Длины медиан и высот треугольника также удовлетворяют трём простым условиям.
Внимание задача! Пусть p, q, r - некоторые положительные числа. Существует ли треугольник у которого биссектрисы равны числам p, q и r соответственно?
Удачи! |
|
|
| номер сообщения: 49-2-389 |
|
|
|
|
MikhailK: Обалдеть. Я похоже нашёл решение задачи, которая меня давно интересовала.
Начну постепенно. Ещё в школе проходят, что длины сторон треугольника должны удовлетворять трём условиям: a<b+c, b<a+c, c<a+b. Длины медиан и высот треугольника также удовлетворяют трём простым условиям.
Внимание задача! Пусть p, q, r - некоторые положительные числа. Существует ли треугольник у которого биссектрисы равны числам p, q и r соответственно?
Удачи! |
Вроде бы очевидно - существуют ..
Или я не прав? |
|
|
| номер сообщения: 49-2-391 |
|
|
|
|
azur: MikhailK: Обалдеть. Я похоже нашёл решение задачи, которая меня давно интересовала.
Начну постепенно. Ещё в школе проходят, что длины сторон треугольника должны удовлетворять трём условиям: a<b+c, b<a+c, c<a+b. Длины медиан и высот треугольника также удовлетворяют трём простым условиям.
Внимание задача! Пусть p, q, r - некоторые положительные числа. Существует ли треугольник у которого биссектрисы равны числам p, q и r соответственно?
Удачи! |
Вроде бы очевидно - существуют ..
|
Любопытно. Почему очевидно? Треугольник существует при произвольных значениях p, q, r?
Возможно я не очень удачно сформулировал условие. При любых ли тройках p, q, r существует треугольник у которого длины биссектрис равны p, q и r соответственно. |
|
|
| номер сообщения: 49-2-392 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|
